計算気象予報士の「知のテーパ」

　今回はちょっと「専門外」のお話です。

　感染症の広がり方を理解するための数理モデルとして「SIRモデル」が知られています。これは「ある閉じられた領域（区画）」の中に存在する人々を、次の３つの状態（S,I,R）に分類して、その時間的な変化を解析するものです。

・未感染者(Susceptible)
　未だ感染していないので、今後「うつされる」リスクがある。

・感 染 者(Infected)
　既に感染しており、今後「うつしてしまう」リスクがある。

・回 復 者(Recovered)
　感染後に回復した状態であり、今後「うつす」ことも「うつされる」こともない。

　つまり、未感染者(Ｓ)→感染者(I)→回復者(R)の順に状態が遷移します。

　これをイメージで表すと、次の図のようになります。


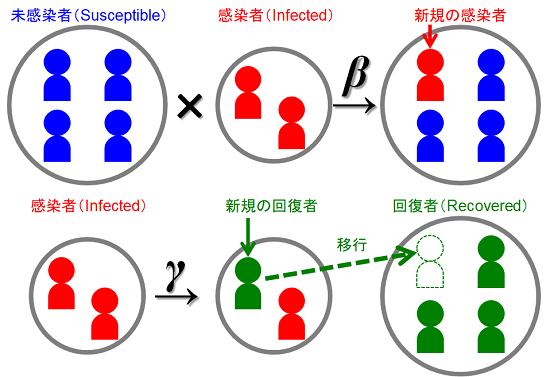
　上の段は「感染過程（Ｓ→Ｉ）」を表しています。

　未感染者と感染者の（直接的な）接触により、感染が起こります。未感染者（うつされる側）の数が多ければ多いほど、また、感染者（うつす側）の数が多ければ多いほど、新たな感染者は増加します。従って、新たな感染者の発生数は未感染者数と感染者数の積に比例すると仮定することができ、その比例定数をβ（感染率）とします。

　下の段は「回復過程（Ｉ→Ｒ）」を表しています。

　これは感染者数の内の一定の割合に相当する数が回復すると仮定しています。このペースを表す比例定数をγ（回復率）とします。

　そこで、第ｔ日目における未感染者数をS(t)、感染者数をI(t)、回復者数をR(t)と書き換えてみると、次の図のように表すことができます。



　第ｔ日目におけるS(t)、I(t)、R(t)の時間的な変化をβ、γを用いて数式の形に表現すると、次のような連立常微分方程式で表すことができます。


　あとは初期条件とパラメータ（β、γ）の値を設定することができれば、数値計算でシミュレーションを行うことができます。（実はこの値の設定が難しい・・・）

　次のグラフは初期条件とパラメータを適当に設定して計算した一つの例です（設定は適当ですが、基本的な特徴は現れています）。


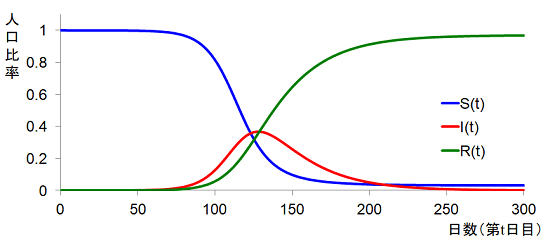
　未感染者数S(t)は時間の経過とともに減少する一方、感染者数I(t)が増加していきます。また、感染者数I(t)の増加に伴って回復者数R(t)も増加します。やがて感染者数I(t)はピークを迎えると、その後は減少傾向に転じます。

　感染者数I(t)に着目すると、次の２点がポイントです（図は省略）。

・感染の拡大が急速であれば、ピーク時の到来は早く、ピーク時の感染者数も増加します。グラフは急峻な形状になります。

・感染の拡大が緩慢であれば、ピーク時の到来は遅く、ピーク時の感染者数は抑制されます。グラフは丘陵な形状になります。


　なお、COVID-19の予測については、（その筋の）専門家が実施・公表されているシミュレーション結果を参照して下さい。この記事が理解のお役に立てれば幸いです。


　ご参考までに、感染症の数理モデルについて詳しく述べられている文献も紹介します。
・西浦 博・稲葉 寿,2006,感染症流行の予測：感染症数理モデルにおける定量的課題, 統計数理（2006）第54巻 第2号,461–480c,統計数理研究所