さて、
「投網暗算法」 の説明です。
この方法で丁寧に計算していけば、
４桁以上の数字同士の掛け算の暗算が可能です。
ただ、計算が計算だけにそれなりの手順は踏みますし、集中力も必要となります。
「ぱっと出来てしまう」という速算法とは異なりますのでご注意ください。
但し、「思ったより簡単だった」ぐらいには感じると思います。
また、「凄く頭の体操になった」とも感じると思います。
では、例題は
１２３４ × ５６７８ としましょう
適当。。。？
。。。 いや、でもちょっと考えました。数字が全て違う方が良いと思ったのです。
それで、これをどうやって計算していくのでしょうか。
基本は、２桁掛け算の際に
４つの四角形を使った考え方、これと全く同じです。
つまり、今回、４桁同士の掛け算となりますので、四角形で言うと ４×４ で
１６個の四角形を考えることになります。
見るからに大変そうです。
本当にやるんでしょうか。
計算としては、１６の四角形を合計するわけですから、
１２３４× ５６７８
＝ １０００×５０００ ＋ ２００×５０００ ＋ ３０×５０００ ＋ ４×５０００
＋ １０００×６００ ＋ ２００×６００ ＋ ３０×６００ ＋ ４×６００
＋ １０００×７０ ＋ ２００×７０ ＋ ３０×７０ ＋ ４×７０
＋ １０００×８ ＋ ２００×８ ＋ ３０×８ ＋４×８
ということになります。
なおさら大変そうに見えてきました。
しかし、順序良く小さなステップを踏んでいけば、いつかは必ず答えは出ます。
先に進みましょう。
先ず、この表を判り易く整理します。
数字で書くと桁が多く大変になるので、漢数字を使いました。
また、
「５６７８」の各数字は右側にもってきました。
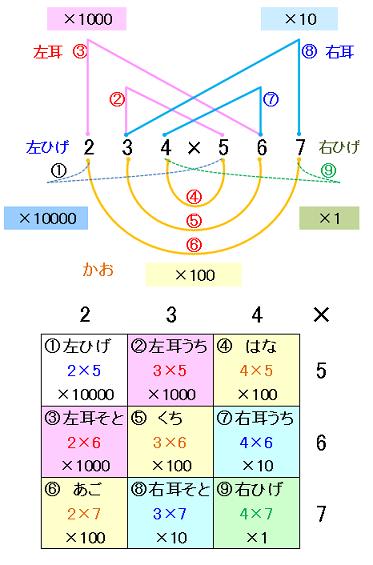
各コマの数字を 「一桁の九九×１０の倍数」で表現すると、
斜めに色分けした駒については、同じ漢数字のグループとなります。
このグループごとに各コマを横に並び変えるとこうなります。
ここで、上記の各組を再度整理します。
百万の組： １×５ × 百万
十万の組： （１×６ ＋ ２×５） × 十万
一万の組： （１×７ ＋ ２×６ ＋ ３×５） × 万
一千の組： （１×８ ＋ ２×７ ＋ ３×６ ＋ ４×５） ×千
一百の組： （２×８ ＋ ３×７ ＋ ４×６） × 百
一十の組： （３×８ ＋ ４×７） × 十
九九の組： ４×８
となります。だいぶすっきりしました。
実は「投網暗算法」においては、この形で計算を行い、一つ一つ足し上げて行きます。
但し、計算式の中で、どことどこの数字同士を掛け算し、足していくのか、
そして何倍するのか、何回それをやったらいいのか、など 良く整理しないと混乱します。
そこで、投網のイメージをつかって順序良く計算するのです。
では、早速暗算の説明に入りたいと思いますが、その前に下準備として紙に下記のように書いて下さい。
左のマス目は、今、計算している組は何なのか、次に計算すべき組は何なのか、
計算した組を何倍すればいいのか、考えるための補助的なものです。
慣れてくれば勿論要らなくなると思います。
マス目の右には計算式そのものを書きます。これは「横書き」です。
この横に並んだ８つの数字を「じぃーっと」にらんで、イメージの中で投網をかけていきます。
投網にかかった数字を一つ一つ丁寧に計算し、合計していきます。
そこで、上記で色分けした組ごとに「投網をかける」のですが、４桁同士の掛け算の場合、
最初は、「千の組」に対して投網をかけます。
「千の組」はこの掛け算のグループでした。
この
千の組に対してかける投網を「千の投網」と呼ぶことにしましょう。
（以降、万の投網、百の投網 等も同様です）
さて、
「千の投網」とは具体的には以下の通りです。
横に並んだ計算式の各数字を線でつないであります。これを「投網」と称していますが、
つながれた数字はそれぞれ「千の組」の中の各コマの掛け算になっています。
つまり、
線でつながれた各数字を掛け算し、合計したのち、千倍することによって、
「千の組」の合計が得られるわけです。
よって、
百の組、万の組等、各組に応じた「投網の掛け方＝線のつなぎ方」を理解すれば、
それぞれの組の合計の出し方が判ります。
その上で、紙に書いた計算式を見ながらイメージの中で投網をかけ、各組の合計を出し、累計をとる。
この手順を繰り返していくのです。
では、以上踏まえまして、各組の「投網の掛け方」を見ながら、暗算の手順を説明します。
<< 投網暗算法 ステップ解説 >>
ステップ１： 千の投網を作り、千の組の合計を出す。
先ず、千の投網を作り、千の組の合計を出します。
千の投網は上図のように、
各数字を外側から１組ずつつなげていけば完成です。
先ずは、ぱぁーっと景気良く全ての数字に投網を掛けるわけです。
投網をイメージとしてかけることが出来たなら、
次は計算です。
線でつないだ各数字を掛け算して、合計します。
そして、「千の投網」ですので、１０００倍します。
ここで、がんばって計算してみてください。
４×５＝２０、それに ３×６＝１８ を足して ３８、それに ２×７ で １４を足して、５２、
最後に １×８ を足して ６０
掛け算の合計は ６０、これに ×１０００ で、千の組合計は ６００００ となります。
この
６００００ をしっかり覚え、次に進みます。
ステップ２： 「万の投網」を作り、万の組の合計を出し、累計する。
次は、「万の投網」に移ります。
順番としては、計算の一番面倒なものから片づけていくという考え方です。
だから、「千の組」の次は大きい方の隣に移って「万の投網」を考えるわけです。
「千の投網」以外の投網は、投網の掛け方が、単純に一番外側から一つずつ、
というわけではありません。どうしたら判りやすいでしょか。
これを混乱なく考えるために、知っておくといいことが一つあります。
この、
投網の線は「交差しない」のです。
あ、そういうこと。。。
つまり、
内側から外側まで、年輪のように拡がっているということです。
よって、この投網の姿を考えるときには
「一番外側の線」を先ず決めれば良いのです。
そこが決まったら、
後は一つずつ内側にずらしながら線を引いて（投網をかけて）いくのです。
しかも
線を何本引くかは位置関係によって自ずと決まるのです。
慣れれば簡単です。
さて、図を見てみましょう。
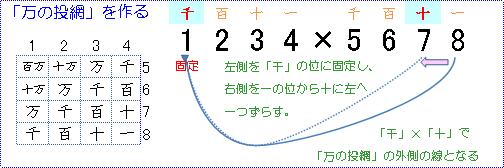
上図のように、一番外側の線を決めるときに、
左側の千の位の数のところ、
これは固定します。これが非常に大事です。
この軸足さえ外さなければ、こんがらがることはありません（大袈裟か。。）
そして、右側の線をどこに引けば「万」の数を作れるか考えます。
（これも考え方として重要です。）
千の位に対しては １０倍すれば「万」となりますので、右側の線は１０の位のところに入ります。
このようにして、先ず、一番外側の線を固めます。
つまり、先ほどの
「千の投網」の一番外側の線の右側を一つ左に「カチッと」スライドさせて
「万の投網」の外側を決める、というイメージで考えて良いでしょう。
同時に投網の横にあるマス目も意識して見て下さい。
どことどこの数字をつなげるか、理解が深まると思います。
一番外側の線が決まったら、次に内側に１つずつずらして線を引きます。
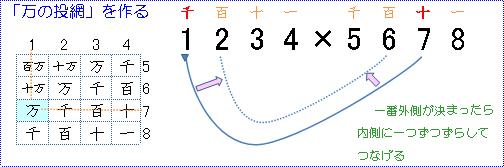
この時は、つないだ線の先数字同士、掛けたら本当に万単位になるのかなんて考える必要はないでしょう。
必ずそうなりますので、ご安心を。機械的に「内側に一本ずらす」 でいいでしょう。
（この「機械的に処理できる」要素が多いほど、計算法としても楽になるのではと考えます。）
「万の投網」の場合、もう一回同じ操作をします。
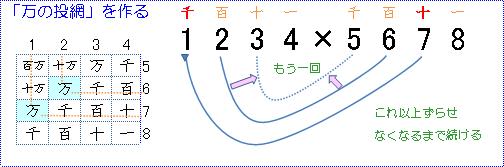
もう、これ以上、引けません。そこで、「万の投網」が完成、ということになります。
このイメージを保持しつつ、同じ線でつながれた各数字同士を掛け算し、それらを合計、一万倍します。
「万の投網」の計算をすると、
今度は外側から考えて、７の、にろく１２で、１９の、さんご１５ごで ３４、か。
で、一万倍だから３４万、さっきの千のやつは、６万だったから、足して ４０万。
うん、ここまでは ４０万。意外とキリのいい数字だ。。。
掛け算の合計は ３４、一万倍して ３４万、
先ほどの
千の組の合計の ６万 を思い出して合計し、 ４０万 とします。
ステップ３： 「百の投網」を作り、百の組の合計を出し、累計する。
次は、小さい側に移って
「百の投網」に移ります。
これも、先ず一番外側の線を確定するわけですが、「百の投網」の場合は、
線の右側、右の数の１の位の部分を固定します。
そして、左側は「百の位」に合わせます。これで外側の線が確定です。
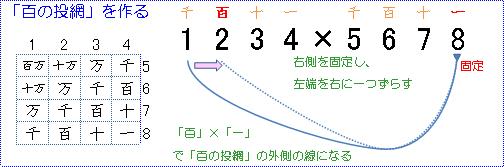
次に、一つずつ内側に線を引きます。
「百の投網」の場合も、これ以上引けなくなるところまで続けます。
３本引いたところで「百の投網」の完成です。
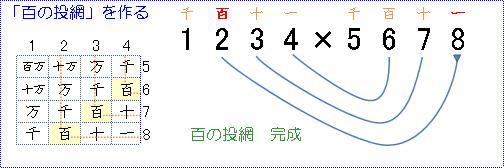
このイメージが持てたら、線でつながれた各数字同士の掛け算し、合計します。
にはち１６ の さんしち２１ で ３７、あと しろく２４ で 合計 ６１ だ。
百倍して ６１００、さっきの ４０万 とたして ４０万６１００ だな。
掛け算の合計は ６１、１００倍して ６１００、
これまでの累計 ４０万 を加えて ４０６，１００、これを覚えます。
ステップ４： 「十の投網」、「一の投網」で下４桁の数を固める。
続いて
「十の投網」を考えます。同様に外側の線は右側を一の位に固定、
左側は左側の数字の十の位とします。「百の投網」から 左側をさらに右へスライドさせて外側の線とします。
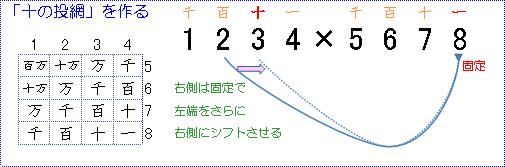
同じように内側に一つずつ線をずらし、
完成します。
ここで再び計算します。
さんぱ２４ の ししち２８、合わせて ５２、×１０で ５２０、
さっきの数字、何だっけ、そう、４０万６，１００ だった。
これに ５２０ をたして ４０万６６２０。。。
掛け算の合計 ５２、１０倍して ５２０、累計は ４０６，６２０ となります。
ここで引き続いて、
「一の投網」までやってしまい、一気に小さい数の方は固めてしまいましょう。
一の投網は左右の各数字、下一桁の数字をつなげます。
しわ３２だから ３２ をたして ４０万６６５２ だ。。。
掛け算は ３２、 累計は ４０６，６５２ となります。
途中経過の数字を記憶しながら、各投網の組の数字を計算するのは大変ですが、
いざ足し算すると
桁の重なりがあまりないので意外と簡単に思えると思います。
また、ここで、万の組 から 九九の組（一の組） まで計算がすみました。
つまり、掛け算の答え下５桁までは固まったことになります。
一旦、下５桁を答えとして書いても良いでしょう。
ステップ５： 「十万の投網」、「百万の投網」を使って最終的な答えを計算。
いよいよ大詰めです。
「十万の投網」に移ります。
手順はもう同じです。外側の線は左の線の位を固定して考えます。
外側の線から内側へ一本ずらし。。
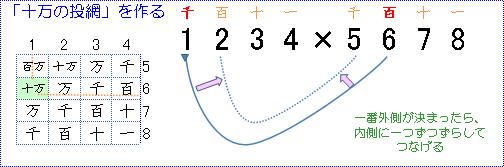
完成です。
あともう少し。。６ と にご１０、ああ、楽、１６ だ。
で、１６十万 だから １６０万か。
何だっけさっきの数字、４０万なんたらだな。あ、ぴったりくる。
２００万と６６５２だ。
掛け算の合計は １６、１０万をかけて、１６０万。
これまでの累計と合計し、２，００６，６５２ となります。
最後に
「百万の投網」です。
今まで計算してきた答えに、ポンと上から大きな数をかぶせます。（
この瞬間がいいですよ）
最後、５００万だ。合わせて ７００万６６２５ これが答えだ。
掛け算の結果は ５、百万倍して ５百万、これまでの累計と合計し、
７，００６，６５２ これを得ます。
お疲れ様でした。
１２３４ × ５６７８ の 答えは ７，００６，６５２ です。
途中の記憶はしんどいですが、
やってやれないことはない、という感じがします。
計算が進むにつれ、記憶する数字の桁も増えてきますが、逆に
投網の計算は楽になっていきます。
これがこの計算法のいいところですね。
いずれにせよ、かなりの頭の体操ですね。
また、この １２３４×５６７８ という問題、途中でキリのいい数字が出てきたりして、
練習としてはいいですね。是非、ご自分でもやってみてください。
あと、 １２３４ × １２３４ もまあまあです。途中経過で楽なところがあります。
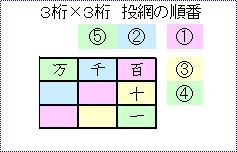
次に、桁数が変わる場合の展開方法として、組ごとの投網をかける順番について考えます。
先ず、全ての数字を外側から一字ずつつなげる投網を一番最初に作るということ、
これは基本です。
最初に一番掛け算の数の多いところをかたずける、というこでしたね。
ちなみに３桁同士の掛け算なら「百の投網」、４桁同士ならば「千の投網」、
５桁同士ならば「万の投網」がその対象となります。
その「総当たり」の組をやったあと、次に一つ大きい組、（４桁なら万の組）、
その後、「総当たり」より小さい組（同、百の組）、これを計算します。
ここまでやったら、今度は数の少ない方を１の位までやってしまい、
その後、大きい側に戻って一番数の組に向かって積み上げていく、という形がいいと思います。
各桁の掛け算において良いと考える図が以下の通りです。
以上が、「投網暗算法」の説明となります。
ひとつ、このブログの使命を果たしたような気もします。ネタ的には最終的なものに近いでしょう。
４桁、５桁の掛け算を暗算したところで、どんなものかとは思いますが、
かなり頭の体操にはなりますし、何より、２桁掛け算の暗算などちょろく感じるようにはなります。
（感じるだけで、進歩しているかどうかは判りませんが。。）
まだ、一生に一度も４桁の掛け算など暗算したこともない、という方、
是非、一度チャレンジしてみてください。今日は何かの記念日になるかも。
人気ブログランキングへ
