こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度灘高入試問題です。
問題は、
「下の図のように、中心がO、半径が1の円Kの周上に点Pをとり、円Kの内部に点Aをとる。
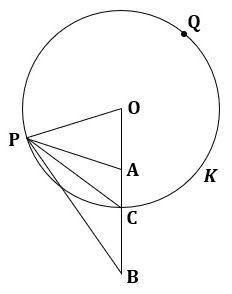
半直線OA上に、線分OAの長さと線分OBの長さの積が1となるような点Bをとる。
(1) △OPB∽△OAP となることを証明せよ。
(2) 半直線OAと円Kの交点をCとおくと、∠APC=∠BPCとなることを証明せよ。
(3) 図のように円Kの周上に点Qをとり、直線PQに関して点Aと線対称である点をDとおくと、△DPB∽△QOB となることを証明せよ。」
です。
図1のように、OA=k とすると、 OA×OB=1 から

です。

▲図1.OA=k とすると、OB=1/k です
そこで、△OPBと△OAP に注目すると、それぞれ、
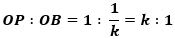
と
OA:OP=k:1
になり、
OP:OB=OA:OP
が成り立ちます。
また、∠POB=∠AOP なので、△OPBと△OAPにおいて、2組の辺の比とその間の角がそれぞれ等しくなることから、△OPB∽△OAP を証明することができました。
次に(2)です。
図2のように、OA=k とすると、
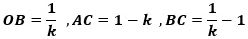
で、PB=l とすると、△OPB∽△OAP から、PA=kl になります。
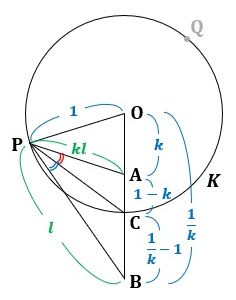
▲図2.OA=k、PB=l として、OB、AC、BC、PAをkとlで表しました
すると、
PA:PB=kl:l=k:1
で、一方、
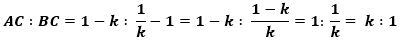
から、
PA:PB=AC:BC
が成り立ちます。
したがって、角の二等分線定理の逆から、∠APC=∠BPC を証明することができました。
最後の(3)です。
図3のように、△OPBと△OAP の相似比をkとすると、
PB:AP=1:k
で、このとき、△PADは二等辺三角形なので、 AP=DP から
PB:DP=1:k [1]
です。
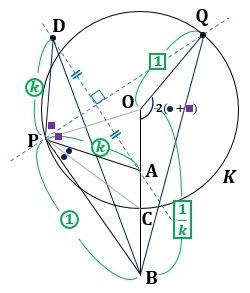
▲図3.△OPBと△OAP の相似比をkとしました
また、
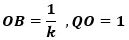
から
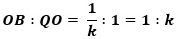
で、これと[1]から
PB:DP=OB:QO [2]
です。
一方、(2)から
∠APC=∠BPC
で、さらに、直線PQが∠APDの二等分線であることから
∠APQ=∠DPQ
になり、したがって、
∠BPD=2∠CPQ [3]
です。
このとき、∠CPQと∠COQはそれぞれ弧CQの円周角と中心角なので、
∠COQ=2∠CPQ
で、∠COQ=∠BOQから
∠BOQ=2∠CPO [4]
です。
したがって、[3]と[4]から
∠BPD=∠BOQ
になり、これと[2]より、△DPBと△QOB において、2組の辺の比とその間の角がそれぞれ等しくなることから、△DPB∽△QOB を証明することができました。
簡単な問題です。
今回は、令和2年度灘高入試問題です。
問題は、
「下の図のように、中心がO、半径が1の円Kの周上に点Pをとり、円Kの内部に点Aをとる。

半直線OA上に、線分OAの長さと線分OBの長さの積が1となるような点Bをとる。
(1) △OPB∽△OAP となることを証明せよ。
(2) 半直線OAと円Kの交点をCとおくと、∠APC=∠BPCとなることを証明せよ。
(3) 図のように円Kの周上に点Qをとり、直線PQに関して点Aと線対称である点をDとおくと、△DPB∽△QOB となることを証明せよ。」
です。
図1のように、OA=k とすると、 OA×OB=1 から

です。

▲図1.OA=k とすると、OB=1/k です
そこで、△OPBと△OAP に注目すると、それぞれ、
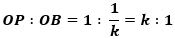
と
OA:OP=k:1
になり、
OP:OB=OA:OP
が成り立ちます。
また、∠POB=∠AOP なので、△OPBと△OAPにおいて、2組の辺の比とその間の角がそれぞれ等しくなることから、△OPB∽△OAP を証明することができました。
次に(2)です。
図2のように、OA=k とすると、
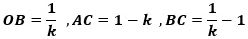
で、PB=l とすると、△OPB∽△OAP から、PA=kl になります。

▲図2.OA=k、PB=l として、OB、AC、BC、PAをkとlで表しました
すると、
PA:PB=kl:l=k:1
で、一方、
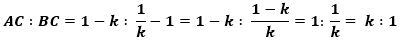
から、
PA:PB=AC:BC
が成り立ちます。
したがって、角の二等分線定理の逆から、∠APC=∠BPC を証明することができました。
最後の(3)です。
図3のように、△OPBと△OAP の相似比をkとすると、
PB:AP=1:k
で、このとき、△PADは二等辺三角形なので、 AP=DP から
PB:DP=1:k [1]
です。

▲図3.△OPBと△OAP の相似比をkとしました
また、
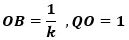
から
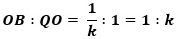
で、これと[1]から
PB:DP=OB:QO [2]
です。
一方、(2)から
∠APC=∠BPC
で、さらに、直線PQが∠APDの二等分線であることから
∠APQ=∠DPQ
になり、したがって、
∠BPD=2∠CPQ [3]
です。
このとき、∠CPQと∠COQはそれぞれ弧CQの円周角と中心角なので、
∠COQ=2∠CPQ
で、∠COQ=∠BOQから
∠BOQ=2∠CPO [4]
です。
したがって、[3]と[4]から
∠BPD=∠BOQ
になり、これと[2]より、△DPBと△QOB において、2組の辺の比とその間の角がそれぞれ等しくなることから、△DPB∽△QOB を証明することができました。
簡単な問題です。




















