【仕様書】最小構成のモデルベース開発事例 その8【離散化後編】

さてと、
テイラー展開第3項まで使用するとどのような式が完成するかって話かな。

まず、第3項までの式はこうなる。
$$f(t)=f(t_0+Δt)=f(t_0 )+f(t_0 ) \frac{d}{dt}Δ+\frac{1}{2} f(t_0)\frac{d^2}{dt^2 } Δt^2$$

今回も定性積分の定義である、\(\int f(t)dt-\int f(t_0)dt\)に対して解きたいので、
両辺を積分する。
$$\int f(t)=f(t_0+Δt)=\int( f(t_0 )+f(t_0 ) \frac{d}{dt}Δ+\frac{1}{2} f(t_0)\frac{d^2}{dt^2 } Δt^2 )$$
$$=f(t_0+Δt)=\int( f(t_0 )+f(t_0 ) \frac{d}{dt}Δ+\frac{1}{2} f(t_0)\frac{d^2}{dt^2 } Δt^2 )$$
$$=\int f(t_o)dt+f(t_0)Δt+\frac{1}{2}f(t_0)\frac{d}{dt}Δt^2$$
あとは移項して、右辺を定積分の形にする。
$$f(t_0)Δt+\frac{1}{2}f(t_0)\frac{d}{dt}Δt^2=\int f(t)dt-\int f(t_0)dt$$

ここで前回の差分法の式を取り出す。
$$f(t_0)\frac{d}{dt}=\frac{f(t_0+Δt)-f(t_0)}{Δt}$$

その通り。
代入するとこうなる
$$f(t_0)+\frac{1}{2}(f(t_0+Δt)-f(t_0)Δt)=\int f(t)dt-\int f(t_0)dt$$

だろうと思って絵を描いた。

そういうこと。
ちなみに、これは台形法という名前が付いている。

まぁ実は式の形については、あんまり考えてなくて、
自分で絵を描けるかどうかという観点でしか解いていない。

絶対的な話ではないけど、以下のイメージでいるよ。
「絵で描ける」→「一定の理屈は通っているはず」→「他者に説明し易い」
例えば、数学的には存在しない式が導出されても、
「絵で描ける」が実現できれば、それはそれで自分自身の公式と言えると思ってる。

というわけで次は微分の方だね。

次は微分に対してテイラー展開第3項までを適用する。

まず、一個前提を追加する。

これまでの前提は以下。
$$f(t)=f(t_0+Δt)$$

ここにもう一個追加する。
$$f(t)=f(t_0-Δt)$$

そうそう。

そして、この二つの前提をテイラー展開に組み込むと以下がでる。
$$f(t)=f(t_0+Δt)=f(t_0 )+f(t_0 ) \frac{d}{dt}Δ+\frac{1}{2} f(t_0)\frac{d^2}{dt^2 } Δt^2$$
$$f(t)=f(t_0-Δt)=f(t_0 )-f(t_0 ) \frac{d}{dt}Δ+\frac{1}{2} f(t_0)\frac{d^2}{dt^2 } Δt^2$$

大正解。

$$f(t_0+Δt)-f(t_0-Δt)$$
をすると第2項だけが残る。
$$f(t_0+Δt)-f(t_0-Δt)=2f(t_0)\frac{d}{dt}Δt$$
そして、\(f(t_0)\displaystyle\frac{d}{dt}\)に対して解く。
$$f(t_0)\frac{d}{dt}=\frac{f(t_0+Δt)-f(t_0-Δt)}{2Δt}$$

絵にするとこう。

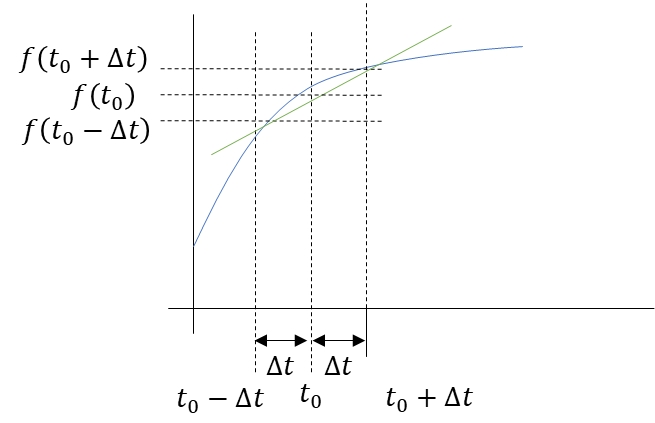
こういうのを中心差分法と呼ぶ。
ちなみに、
前回やった\(f(t_0+Δt)\)で解いたパターンだと前進差分法、
やってないけど\(f(t_0-Δt)\)で解いたパターンだと後進差分法、
って呼ぶよ。

そうだね。
ここまでだと比較的説明し易いし、
それほど演算負荷も上がらないから割と使われていることは多いね。

そうだね。そこは次回やってみよう。

まとめだよ。

• テイラー展開第3項までを使用した積分近似手法は台形法と呼ばれる。
• テイラー展開第3項までを使用した微分近似手法は中心差分法と呼ばれる。
  • \(f(t_0+Δt)\)で解いたパターンだと前進差分法。
  • \(f(t_0-Δt)\)で解いたパターンだと後進差分法。
• 数式を解く場合は、「絵を描けるか」という観点で解くと迷わなくて良い場合がある。
  • 納得もできるし、説明もし易い。

フクさん：
離散化の話で3回に渡ったんで、それのまとめ。

• ぶっちゃけ総和法と差分法だけ知ってればOK。(初歩)
• しかし、それらの向こう側も知っておく必要がある。(原理)
• そして、知った上で不要と判断して意図的に捨てる。(基礎)

という感じのアプローチを意識できていれば、
変に初歩で止まって応用が利かないということは起こりにくくなる。