高校数学での範囲での積分による体積計算の方法について説明します。
積分と体積の関係
1変数の関数の積分が基本的にはグラフ上の面積を表すのに対し、2変数関数の2重積分は体積に対応します。(座標上のスカラー関数を体積積分する場合などは3重積分。)【※高校数学の微積分の範囲外。】
他方で、2重積分の最初の積分、「面積」に該当するところが積分以外の方法でS(x)という形の関数で表せるのであれば、これについての1変数の積分として体積を計算する事も可能な場合があります。錐体の体積や球の体積など、基本的な立体図形の体積公式はこの考え方でも導出できます。
例えば、断面の形が三角形、四角形、円などの規則的で容易に面積を計算できる図形であれば断面積を積分によらずに出せるので、それを1変数関数で表し積分すれば体積になるというわけです。
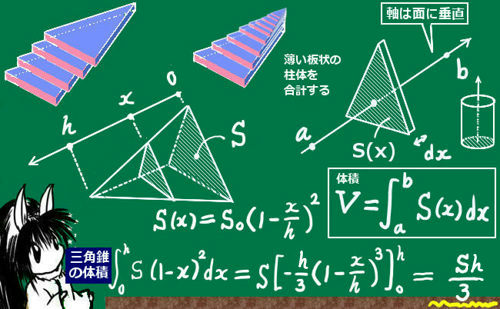
立体の断面がS(x)で表され、変数xの軸が断面に垂直である時、体積Vは次のように表されます:$$V=\int_a^bS(x)dx\hspace{15pt}(a,b\hspace{3pt}はてきとうな定数)$$
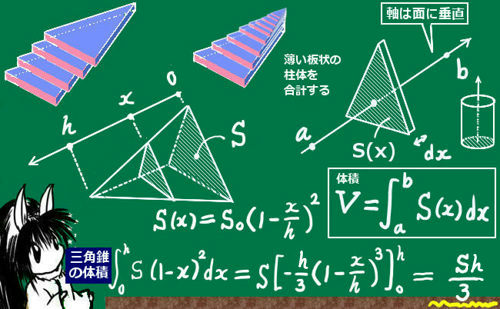
計算の注意点としては、明確に「体積」なるものを計算したい場合には、きちんと断面に対する「高さ」に対応するように軸の向きをとる必要があるという事です。そうしないと計算しても変な値になってしまい、正しく体積を計算できません。
積分で体積を計算できる根拠は、「薄い錐体」(三角柱、四角柱、円柱など)を加え合わせ極限をとるという操作を体積計算とみなしているためだからです。
例えばある立体の断面をもとに体積を考えたいときには、基本的に軸はその断面に垂直になるようにとって積分を計算する必要があります。
【※じつは軸は必ずしも直線でなくてもいいのですが、その場合でも断面に垂直である必要があります。】
積分の記号「∫f(x)dx」はこれ全体で1つの意味を表すと捉えるべきですが、もともとの考え方から言うとf(x)と(微小な)区間の幅dxの積を加えて区間の数→無限、dx→0という極限を考えたものでもあります。従って、断面積を関数として積分している時点で、「断面積×微小な高さ」という、微小な柱体の体積を考えている事になります。
しかしそこで本来「高さ」にはならないものを軸にして変数を考えてしまうと、積分の結果もおかしくなってしまい実際の体積を正しく表せない・・という事です。
錐体の体積公式【積分による導出】
三角錐、四角錐、円錐の体積公式:「体積=底面×高さ÷3」は、積分で導出できます。
【※それとは反対に、積分を使わなくても導出は一応可能です。】
一番下の底面に平行な平面による錐体の断面を考えてみましょう。最も基本的なのは三角錐なので、まずそれで考えます。
断面によってできる側面の線は、底面に平行になります。このとき、もとの側面の三角形と相似な三角形が作れて、相似比はどの側面でも同じ事に注意します。すると、断面の三角形は底面の三角形に相似であって、面積比は相似比の2乗になります【相似比と面積比の関係】。
この相似比はどこの高さで断面を考えているかによって決まります。そこで、高さの範囲を [0,h]とします。hは三角錐全体の高さです。ある高さxでの断面の三角形の1辺は、底面の1辺の1-x/h倍です。例えば3/hの高さであれば2/3倍という事です。4/hの高さなら3/4倍です。
相似比が1-x/hなので、面積比は(1-x/h)2です。
底面積をS(定数)とすれば、断面積はS(1-x/h)2という事になり、これを0~hで積分すれば体積を得るという仕組みです。

$$\int_0^hS\left(1-\frac{x}{h}\right)^2dx=\left[-\frac{h}{3}\cdot\left(1-\frac{x}{h}\right)^3\right]_0^h=\frac{Sh}{3}$$
この通り、結果は「底面積」×「(底面から測った立体的な)高さ」÷3になります。
原始関数を出すところが多少込み入りますが、原始関数を微分すると合成関数の微分で-3/hが掛けられます。そこから逆算して-h/3を係数としてつけているわけです。
代入するところの計算は、hを代入すると1-x/h=0で, 0を代入すると1-x/h=1になる事により結果の式を出しています。【このため、結果の式では「3乗」というものがあった事は見えなくなり、1/3という係数だけが痕跡として残っているような形になります。】
ところでこの計算を見ると、底面積はSという一般的な形をしていて三角形に限っていません。問題は、高さxでの相似比と面積比という事になりますが、これは任意の多角形で成立する性質です【多角形は三角形に分割できるため】。
そのため、この積分計算は多角錐でも適用できる事になります。
また、円錐の場合でも適用できます。円を多角形の近似と考えてもいいですし、三角形の相似から半径が1-x/h倍になり、円の面積は半径の2乗に比例するからと考えても結果は同じです。
そのようにして、三角錐に限らず、他の多角錐や円錐でも体積公式は同じであるという結果を得るのです。
回転体の体積
高校の微積分では、一般的に「関数を軸周りに回転させてできる図形(回転体)の体積」を計算させる問題が多く問われます。
事の本質は「断面積をxの関数で表し、断面に垂直な方向に積分すれば体積」という事です。
軸の周りに回転させるという事は、断面は必ず円になります。y=f(x)で表されている時、これそのものを変数xにおける「半径」と考えて、断面積をxで表すというわけです。
$$S(x)=\{f(x)\}^2として積分\hspace{20pt}V=\int_a^b\pi{f(x)}^2dx$$
これは、公式を暗記するのではなくて、意味を覚えて普通に計算する方が断然楽である部類の積分の計算の1つです。「要するに断面積を変数で表す事が必要」という事だけ覚えて、あとは図形的に判断すれば計算が可能です。
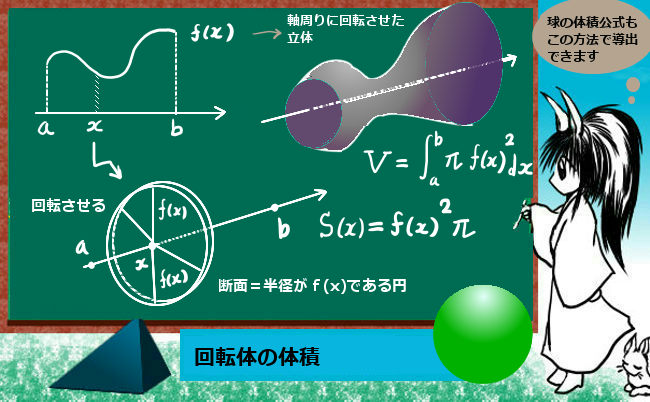
この「回転体の体積」を積分で計算する事の応用例で重要なのは球の体積公式です。この場合は、円の式x2+y2=r2からy=・・の形に直して2乗し、積分するという事になります。
ただ、高校数学の微積分の問題だと、応用上の重要度というのは度外視して、よく分からない関数を回転させて体積計算させるという問題も少なからず見かけます。
高校数学での出題では、あくまで積分の基本計算を正確にできるかを問うていると捉えるべきでしょう。
大学入試の場合には2つのグラフで囲まれる部分を回転させるといった出題もあります。この場合、グラフ同士の交点を出さないと積分区間が分からないので、積分単独ではなく複合的な形の問題になっています。