2024年3月10日(日)
岐阜県の公立高校の入学試験が3月5日(一部は、6日も実施)に行われた。私は毎年ブログに数学の問
題と県教委からの解答、そして私自身が解いて方法による解説を掲載している。今年も、ブログに載せるこ
ととした。
ただし、私自身忙しくてじっくり考えて解いている時間的余裕がなかった。数学の問題と県教委からの解
答や出題のねらいは、岐阜新聞の朝刊から引用させていただいた。切り貼りで、読みにくい状態になった。
また、私自身の解答は、ノートに殴り書きなような状態になった。手書きで、十分見直しをすることもでき
なかったので、誤字・誤植の類や他の面で誤りがあったらご容赦願いたい。
まず、全体的な感想を述べる。2~3年前に比べるとやさしかったとの印象である。平均点も50点前後
であろう。それでも、中学生が解くのに難しいだろうと思う問題が3~4問あった。具体的には、次の問で
ある。
大問4の(5)、大問5の(2)の(イ)、大問6の(2)のイ~エ、大問6の(3)
私の解答で、大問5の(2)の(イ)と大問6の(2)のイ~エは、高校数学的な解き方になった。大問6
の(3)は、△OAPの3辺a,b,cとしたとき、最大辺がaのとき、
b²+c²>a²
を使って解こうと思ったがうまくいかなかった。中学数学の解法で、いい方法があったらご教示していただ
きたい。
数学の入試問題


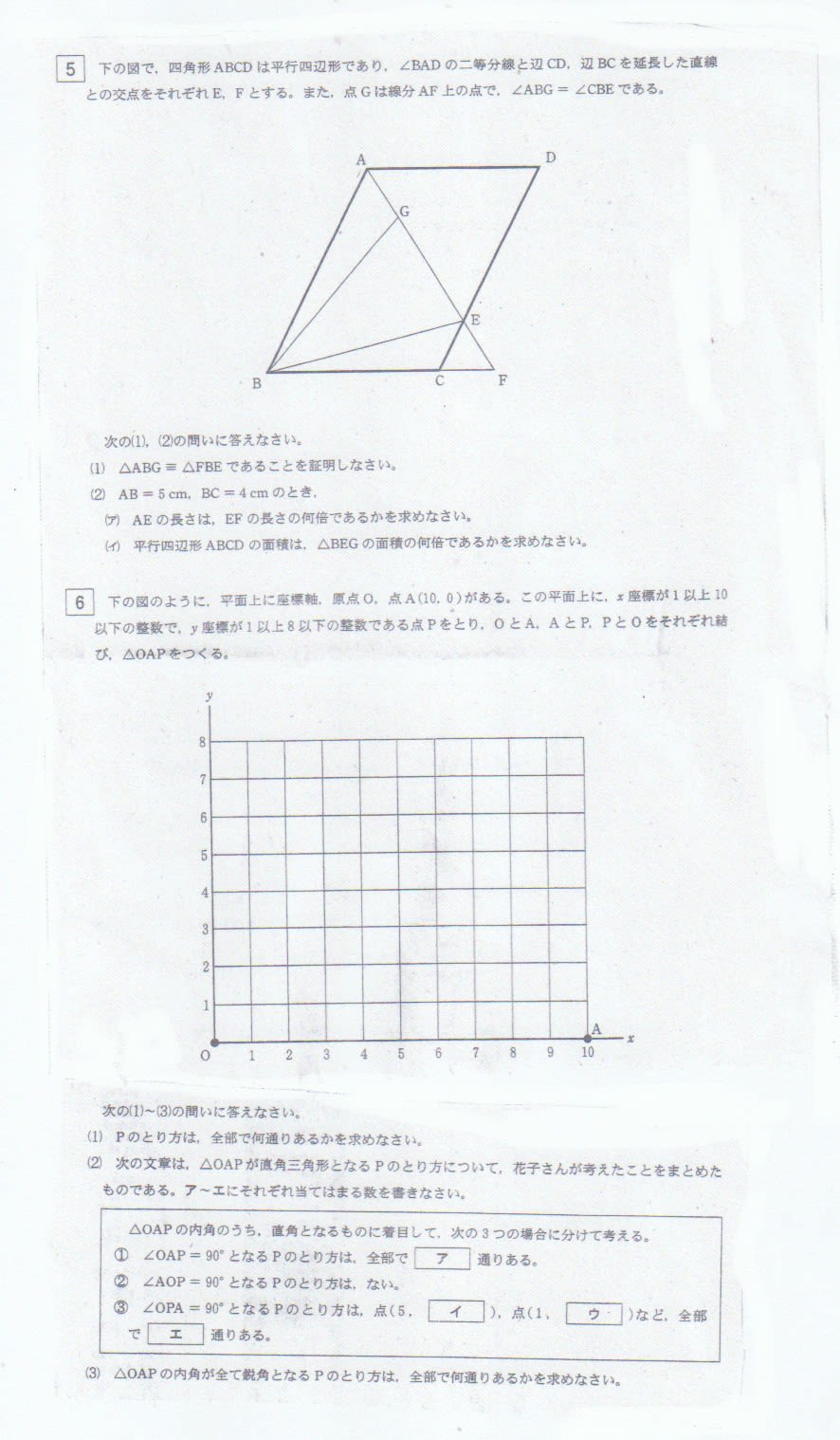
配点及び解答
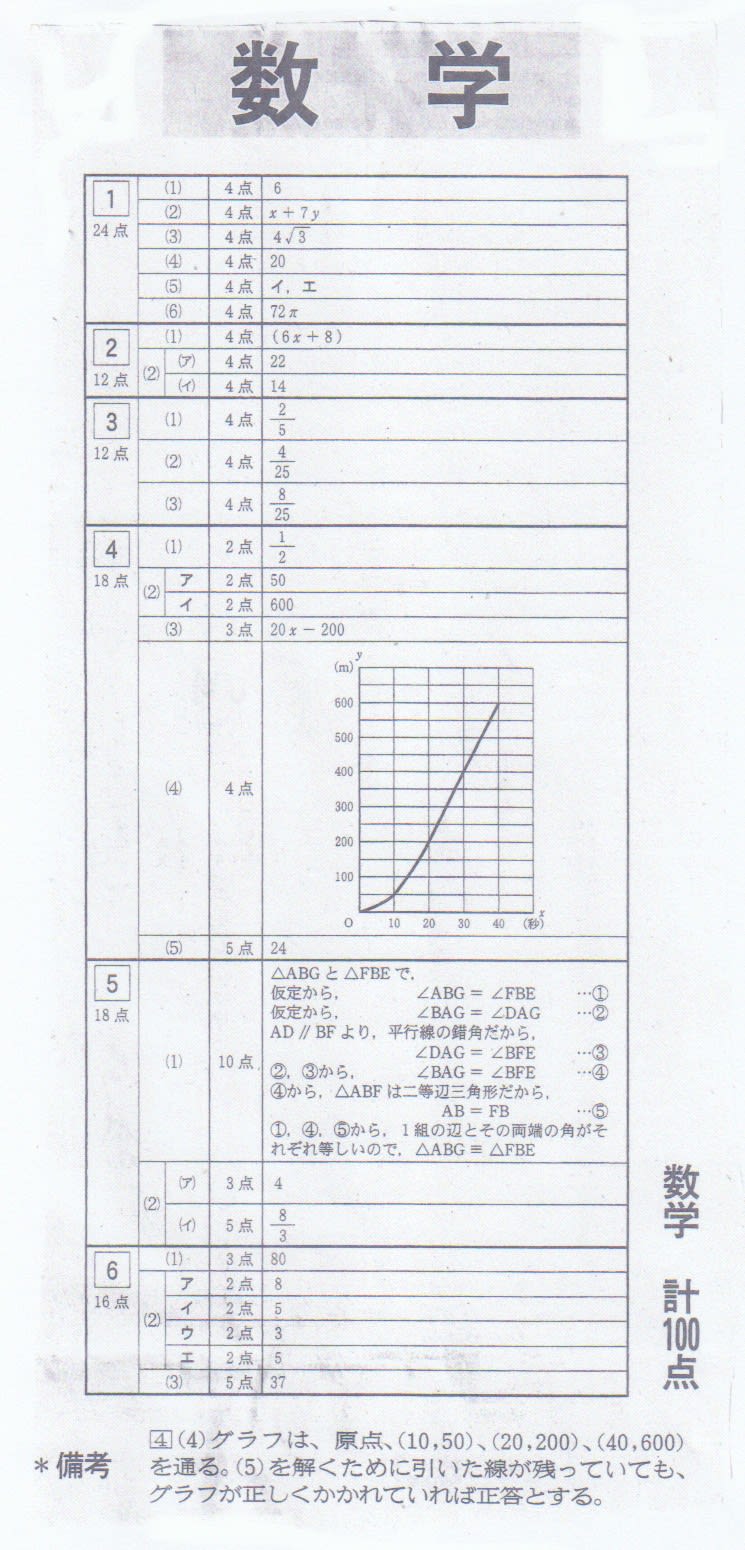
県教委による出題の意図

解説

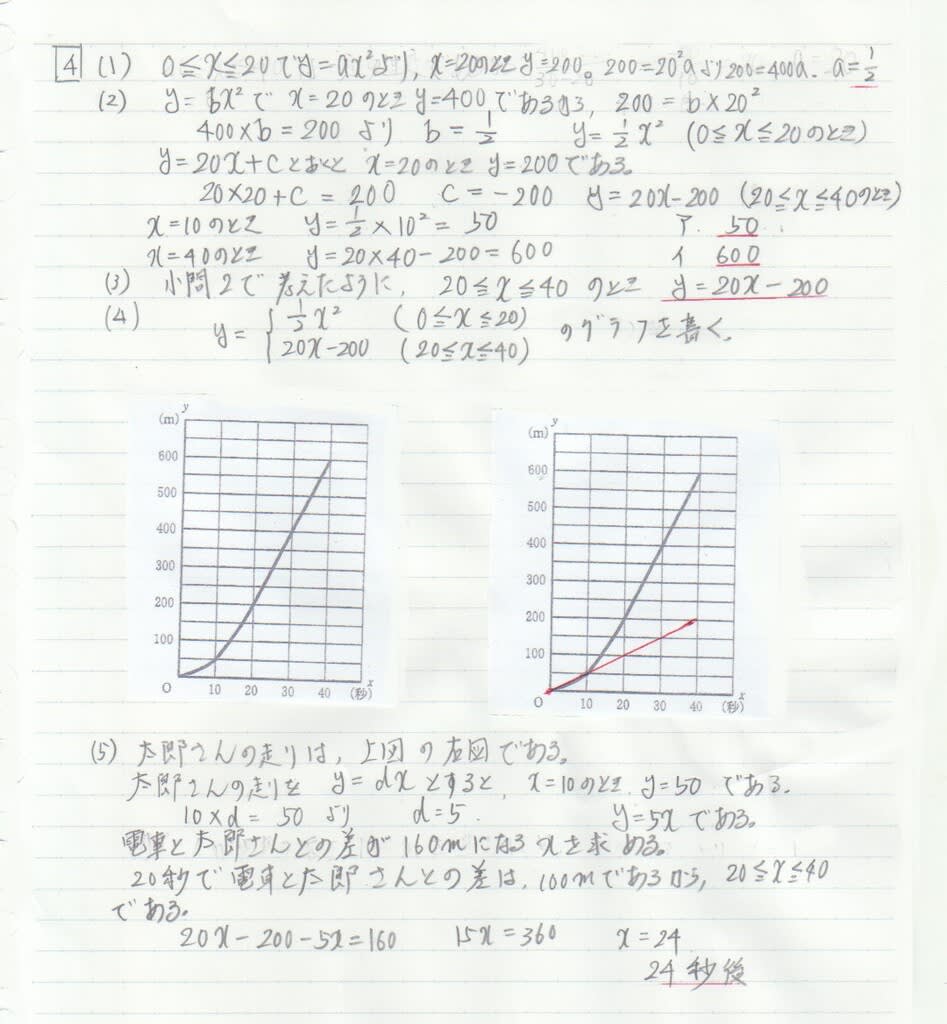

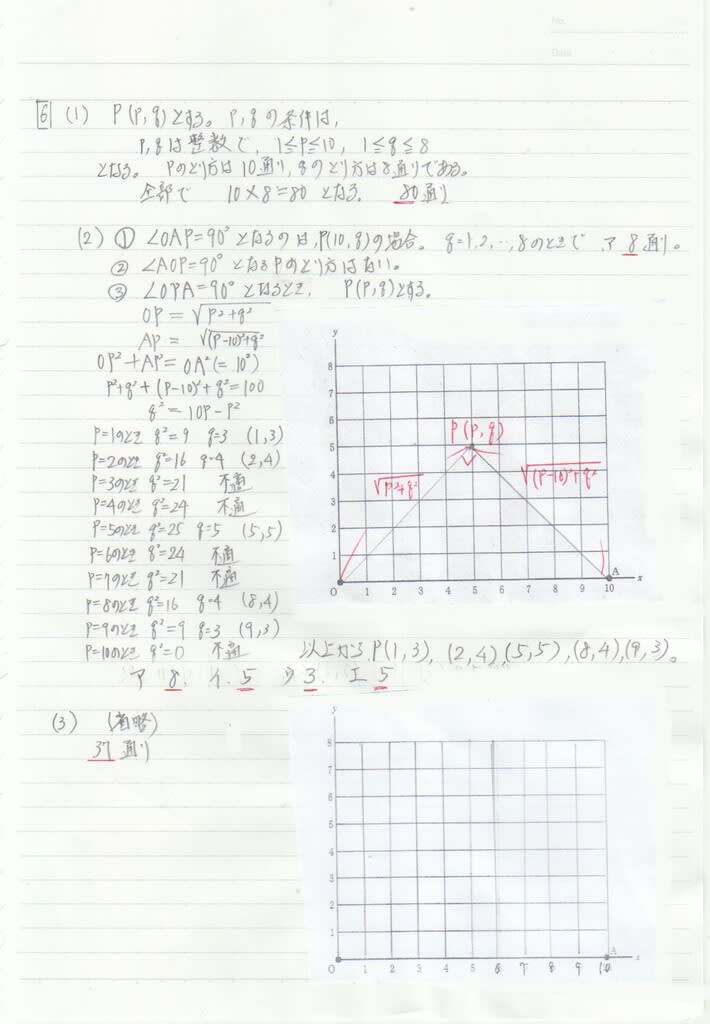
注意1
大問6の「お助けマン」氏の解法を、コメントを引用することで紹介しておこう。
・・・・・・・・・・・・・・・・・・・「お助けマン」氏より・・・・・・・・・・・・・・・・・・・・
大問6の(3)ですが、次の方法で解く事ができました。それは、鋭角三角形の一番長い辺をa、残りの二辺
を、それぞれ、b、cとしますと、鋭角三角形の条件は、a²<b²+c²が成り立ちます。これを使って解く事ができ
ました。今回の問題では、鋭角三角形になるためには、y≧4となります。
この中で、y≧5は、Pが(5,5)は除きますと、9✕4−1=35となります。そして、y=4の場合は、Pが(1,4)と
(9,4)は10²<(√1²+4²)²+(√9²+4²)²→100<17+97が成り立ちます。そして、(9,4)も同様に100<97+17が成り
立ちますので、合計2個を追加します。よって、求める式は、9✕4−1+2=37と求まります。
よって、答えは、37通りとなります。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・「お助けマン」氏より・・・・・・・・・・・・・・・・・・・・・・
前回の投稿では、大問6の(3)の解法に、鋭角三角形の条件のa²<b²+c²を用いて解いてみました。
今回は、鋭角三角形の条件を知らない中学生が、解く事が出来る別解を考えてみました。
まず、鋭角三角形になるには、y≧4が成り立つ事を示したいと思います。先生のご教示の通り、y≦3はすべて
鈍角三角形になります。これは作図より明らかであります。すると、鋭角三角形になるには、y≧4と推察出来ま
す。そこで、Pが(5,5)ですと、直角三角形になるので、鋭角三角形は、−1となります。そして、直径10の半円
周の作る角度は、90°ですが、半円周の外の頂角は、鋭角になるので、y≧5の時は、4✕9−1=35となります。
また、y=4の時、直径10の半円周の内側にある頂角は、鈍角になるので、(3,4)〜(7,4)までの5個の三角形は、
鈍角三角形になります。また、(1,4)と(9,4)は、直径10の半円周の外なので、鋭角三角形になります。そして、
(2,4)と(8,4)は、直角三角形である。よって、y≧5の35個の鋭角三角形に2個の鋭角三角形を加えて、求める式
は、4✕9−1+2=37となります。よって、答えは37通りとなります。
以上ですが、今回は、鋭角三角形の条件は用いずに、直径10の半円周の外の頂角は鋭角になり、直径10の半円周
上は直角になり、直径10の半円周の内側の頂角は鈍角となる関係を用いて解いてみました。これですと、中学生も
理解出来るかと思い、投稿しました。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
注意2
「最大辺をaとすると、b²+c²>a² ⇔ 鋭角三角形」 は高校の数学Ⅰですぐに証明できる。余弦定理から、
(b²+c²ーa²)/2bc=cos A>0
が成り立つからである。
ちょっと休息
(1)卒業式・修了式
中学校の卒業式が大垣市では3月7日に、海津市では3月8日に行われた。
海津市の小中学校の修了式・離任式は、3月22日 (金)に行われる。海津地内5小学校の新設統合
の準備等(25・26)で、早めの修了式になったようです。多くの市町村では、3月26日(火)の実
施だと思う。小学校の卒業式は、その1日前である。
(2)しだれ梅の開花 3月8日のfacebook投稿より
しだれ梅が咲きました。何年か前に枯れかけて切り倒そうとした梅です。太い幹から芽が出てきて、
見事生き返りました。

















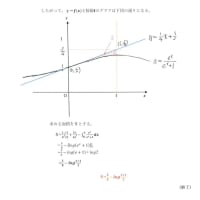












大問4の(1)ですが、間違いを見つけました。0≦X≦20の範囲では、y=aX²が成り立つので、y=aX²にX=20、
y=200を代入すると、200=a✕20²、400a=200よって、
a=1/2となり、答えは、a=1/2かと思います。いかがでしょうか。ご確認をお願いします。
それと、大問6の(3)の問題ですが、今、悪戦苦闘しながら、解いています。もし、解けた場合は、紹介させていただきたいと思います。これからも宜しくお願いします。お助けマンより。
ご指摘のあった大問(4)の(1)の誤りは、訂正しておきました。求めるものが直線と勘違いしていました。放物線の方です。
>大問6の(3)の問題ですが、今、悪戦苦闘しながら、解いています。もし、解けた場合は、紹介させていただきたいと思います。
⇒よろしくお願いします。何か大事なことに気づいていないから解けないのかも知れません。
さて、大問6の(3)ですが、次の方法で解く事ができました。それは、鋭角三角形の一番長い辺をa、残りの二辺を、それぞれ、b、cとしますと、鋭角三角形の条件は、a²<b²+c²が成り立ちます。これを使って解く事ができました。今回の問題では、鋭角三角形になるためには、y≧4となります。この中で、y≧5は、Pが(5,5)は除きますと、9✕4−1=35となります。そして、y=4の場合は、Pが(1,4)と(9,4)は10²<(√1²+4²)²+(√9²+4²)²→100<17+97が成り立ちます。そして、(9,4)も同様に100<97+17が成り立ちますので、合計2個を追加します。よって、求める式は、9✕4−1+2=37と求まります。よって、答えは、37通りとなります。ご確認いただけますと嬉しく思います。ただ、今回の入試では、鋭角三角形の条件のa²<b²+c²の関係は、高校で扱うかと思いますので、図に書いて考えて解答出来た生徒は、かなり少ないかと予想します。正答率は低いかと思いますが、いかがでしょうか。ご教示いただけますと嬉しく思います。これからも宜しくお願いします。お助けマンより。
9+25<49なので、鈍角三角形と言えます。また、3cm、4cm、5cmならば、3²+4²□5²→9+16=25より、直角三角形と言えます。6cm、8cm、9cmならば、6²+8²□9²→
36+64>81より、鋭角三角形と言えます。このように、三平方の定理を利用して、鋭角三角形か、直角三角形か、鈍角三角形かの同定が出来ますので、今回の入試問題に適用してみました。これについてのご教示をいただけますと、とても嬉しく思います。宜しくお願いします。お助けマンより。
前文の最後に誤りがありました。
誤 b+c>a →正 b²+c²>a²
実は、私も「お助けマン」氏と同じ考えで解こうとしましたが、y≦3にも鋭角三角形になる場合があるのではないかと思っていたのです。よく考えてみると、y=1はすべて鈍角三角形、y=2もすべて鈍角三角形、y=3は(1,3)(9,3)と(10,3)が直角三角形,それ以外は鈍角三角形となります。鋭角三角形が表れてくるのは,y≧4となります。あとは、「お助けマン」氏の通りです。改めて考えてみると、「y≦3にも鋭角三角形になる場合があるのではないかと思っていた」ことが誤りでした。
「最大辺をaとすると、b²+c²>a²⇒鋭角三角形」 は高校の数学Ⅰですぐに証明できます。余弦定理から、
(b²+c²ーa²)/2bc=cos A>0
が成り立つからです。
ありがとうございます。
そこで、今回は、別解として、鋭角三角形から、直角三角形と鈍角三角形を合わせて引く方法で、解いてみたいと思います。鋭角三角形は、y≧4から、9✕5=45通り。
その中で、y=5の時、(5,5)は直角三角形。y=4の時、(2,4),(8,4)は直角三角形、また、(3,4)(4,4)
(5,4)(6,4)(7,4)は鈍角三角形の合計は8通りより、求める式は、9✕5−8=45−8=37、よって答えは、37通りである。
以上ですが、今回の問題は、鋭角三角形、直角三角形、鈍角三角形の成立条件を用いて解きましたが、中学生にとっては、難しい問題かと思います。もし、大問6の(3)の正答率が10%を切ったならば、問題作成の検討・吟味が必要な問題かとも思います。2、3年前の難しい問題と比べて、今回は、比較的解きやすい問題は多かったが、平均点は、やはり55点以上は、欲しい所であります。これからも岐阜県の公立高校入試の難易度の状況を見守っていきたいと思います。これからも宜しくお願いします。お助けマンより。
今回は、鋭角三角形の条件を知らない中学生が、解く事が出来る別解を考えてみました。まず、鋭角三角形になるには、y≧4が成り立つ事を示したいと思います。先生のご教示の通り、y≦3はすべて鈍角三角形になります。これは作図より明らかであります。すると、鋭角三角形になるには、y≧4と推察出来ます。そこで、Pが(5,5)ですと、直角三角形になるので、鋭角三角形は、−1となります。そして、直径10の半円周の作る角度は、90°ですが、半円周の外の頂角は、鋭角になるので、y≧5の時は、4✕9−1=35となります。また、y=4の時、直径10の半円周の内側にある頂角は、鈍角になるので、(3,4)〜(7,4)までの5個の三角形は、鈍角三角形になります。また、(1,4)と(9,4)は、直径10の半円周の外なので、鋭角三角形になります。そして、(2,4)と(8,4)は、直角三角形である。よって、y≧5の35個の鋭角三角形に2個の鋭角三角形を加えて、求める式は、4✕9−1+2=37となります。よって、答えは37通りとなります。
以上ですが、今回は、鋭角三角形の条件は用いずに、直径10の半円周の外の頂角は鋭角になり、直径10の半円周上は直角になり、直径10の半円周の内側の頂角は鈍角となる関係を用いて解いてみました。これですと、中学生も理解出来るかと思い、投稿しました。ご確認いただき、先生のご教示を賜わりますと、嬉しく思います。宜しくお願いします。お助けマンより。
>直径10の半円周の作る角度は、90°ですが、半円周の外の頂角は、鋭角になる・・・
⇒おそらく、出題者の意図は素期にあると思います。
直径をOAを半径とする点P(5,5)を通る半円を書いたとき。その半円の外側に点Pをとると、△OAPは鋭角三角形になります。その半円の外側Pの点を数えればいいわけです。正しいと思います。
最近忙しいので高校入試問題については、今は考えていません。ご教示、ありがとうございます。